jcalcutt.github.io __main__
Interview Questions
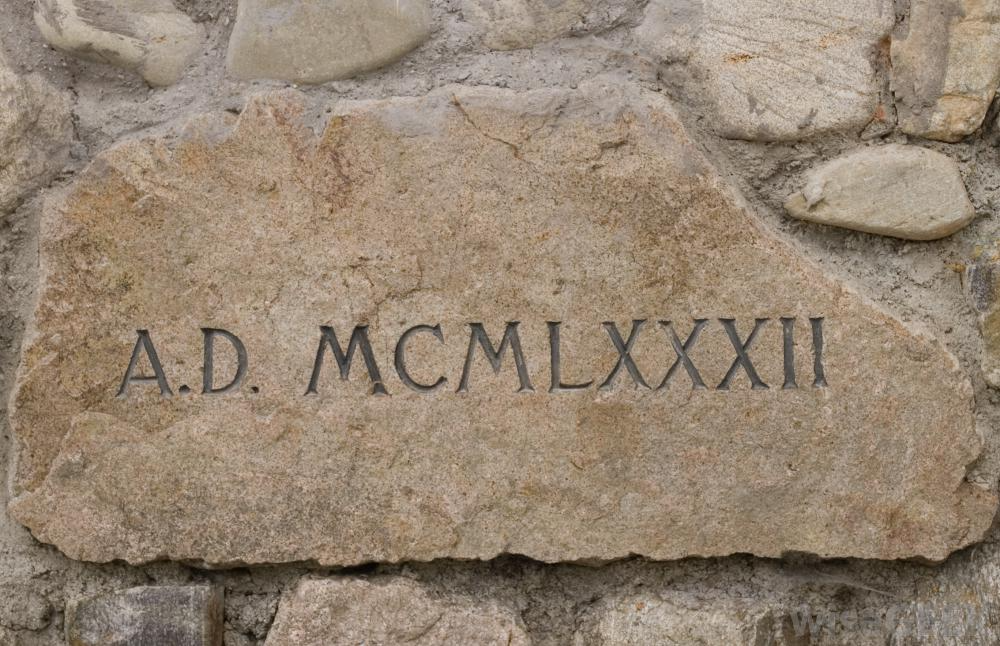
Coding Interview Questions. Time-pressured, no-googling tasks that you are not likely to encounter in your usual day-to-day - but are used to help determine if you’re suitable for the job. I’ve (succesfully!) encountered a few of late, so I’ve picked a selection of my ‘favourites’ to walk through.
1. Roman Numerals
Given a year, convert it to its Roman Numeral representation. I won’t go into too much depth here about the underlying logic of how numbers are converted to Roman Numerals (you can look that up here). However, to keep it simple, we have to bear in mind that certain numerals are concatenated together to create larger numbers (i.e. 3 is III), or other numerals placed to the left or right of larger numerals to add or subtract from that number (i.e. 4 is IV, 40 is XL, 45 is XLV).
Here’s my solution:
symbols = {
1:"I",
5:"V",
10:"X",
50:"L",
100:"C",
500:"D",
1000:"M"
}
def numerals(n: int) -> str:
"""Given an integer year from 1-3000, convert it to roman numerals
Parameters
----------
n : int
year to convert, valid from 1-3000, e.g. 1975
Returns
-------
str
Roman numeral representation of the requested year, e.g. MCMLXXV
Raises
------
ValueError
Year passed is too large
"""
result = []
sn = str(n)
x = len(str(n))
if n > 3000:
raise ValueError("Unable to handle year this large")
# milleniums
if x == 4:
# standalone logic to create the millenium numerals
result.extend(symbols[1000]*int(sn[-4]))
# check how many digits we have, and if we do, pass that digit to the numeral conversion logic
# centuries
if x >=3:
result.extend(numeral_logic(int(sn[-3]), symbols[100], symbols[500], symbols[1000]))
# decades
if x >=2:
result.extend(numeral_logic(int(sn[-2]), symbols[10], symbols[50], symbols[100]))
# years
if x >=1:
result.extend(numeral_logic(int(sn[-1]), symbols[1], symbols[5], symbols[10]))
# convert to string and return
return "".join(result)
def numeral_logic(value: int, small: str, mid: str, large: str) -> str:
""" For a given number, and set of small, mid, and large numeral mappings, implement the roman numeral conversion logic.
Valid for centuries, decades and individual years.
Parameters
----------
value : int
century, decade, or year to convert to numeral
small : str
small unit for the value, e.g. "C" for a century value
mid : str
mid unit for the value, e.g. "D" for a century value
large : str
large unit for the value, e.g. "M" for a century value
Returns
-------
str
roman numeral representation for the requested value, e.g. "IV" for 4
"""
if value <= 3:
result = small*value
elif value == 4:
result = small + mid
elif value == 5:
result = mid
elif value > 5 and value <= 8:
n = value-5
result = mid + n*small
else:
# value = 9
result = small + large
return result
https://gist.github.com/jcalcutt/1c147f818f7118d3d4f1d2666f517058
We iterate over each value in the integer year we’re passed (by converting to a string), apply the logic to convert that value to a numeral, append to a list, then finally concatenate that into one string and return.
My high-level thought process, was to treat each digit in the ‘overall’ year in isolation. We need to know which value in the year we’re dealing with: the millennium, century, decade or ‘individual’ year. We also need to be flexible, as we could be passed e.g. the year: 25, 225, or even 2025.
With that in mind, Millenniums are treated in isolation and we just multiply the Roman Number representation of 1000 (“M”) by the millennium number i.e. 3 becomes “MMM”.
Next, and the key step to all of this, was that I realised the logic to covert a century, decade or individual year is exactly the same and can be abstracted to one function. The difference between each one we’re interested in just boils down to the numerals we’re manipulating and can be passed as variables to this helper function. For example, the logic to convert the century 4 or the decade 4 is the same, it just involves different numerals: the century 4 uses “C” and “D” to form “CD” and the decade 4 uses “X” and “L” to form “XL”.
Congrats if you converted the main header image to 1982…
2. Max Palindrome
Given a string of letters, find the longest palindrome substring that can be created out of them - i.e. a string which is exactly the same backwards as it is ‘forwards’. Preference should be given to alphabetically ‘smaller’ values if multiple solutions exist. For example, a given string of “aaabbb” should return: “ababa”, not “babab”.
Again, here’s my solution:
def maximal_palindrome(s: str) -> str:
"""Given a string of letters, find the maximum length possible palindrome
Parameters
----------
s : str
input string of letters, e.g. "abaacc"
Returns
-------
str
maximum palindrome, e.g. "acaca"
"""
result = []
s = s.strip()
unique_letters = ''.join(set(s))
unique_letters_sorted = sorted(unique_letters)
# create a dictionary of letter counts we have for each unique letter
letter_count_dict = {}
for letter in unique_letters:
letter_count_dict[letter] = s.count(letter)
# loop over the sorted list of letters
for letter in unique_letters_sorted:
# if we have more than one letter, add n/2 of those letters to result list
# update letter count dict acordingly
if letter_count_dict[letter] >= 2:
equal_num_available = int(letter_count_dict[letter]/2)
result.append(letter*equal_num_available)
letter_count_dict[letter] -= 2*equal_num_available
# add leftover smallest letter - to be added to the middle
leftover_smallest = ""
for letter in unique_letters_sorted:
if letter_count_dict[letter] > 0:
leftover_smallest = letter
break
# create final result, since we added n/2 of each unique letter above,
# we can just reverse that list
result = result + [leftover_smallest] + result[::-1]
# convert to string and return
return "".join(result)
https://gist.github.com/jcalcutt/5201c695fa0b0707ac885e3e826b9d6f
Now, this isn’t the ‘purest’s’ way of solving this problem. I’ve done some research, and Manacher’s algorithm is considered the best approach here, bringing down the time complexity to an impressive O(n). Anyway, my first steps here were to create a sorted string of the unique letters we’re passed, and also create a letter count mapping dictionary. The logic to build up the palindrome was fairly simple: we loop over each character in the sorted string, if we have 2 or more ‘counts’ of this letter we add the count/2 (rounding down) times of that letter to a list. Next, we then update the word count dictionary, reducing the count number by 2x the number of that letter we’ve added to the list.
Once that’s done, we’re pretty much finished. The penultimate step is to check if we have any ‘extra’ letters we can add to the middle of the palindrome - using the smallest alphabetical letter. Finally, we then concatenate; the list, the smallest alphabetical letter (if we have one), then the list again in reverse, convert it all to a string and return.
3. Word Count Board
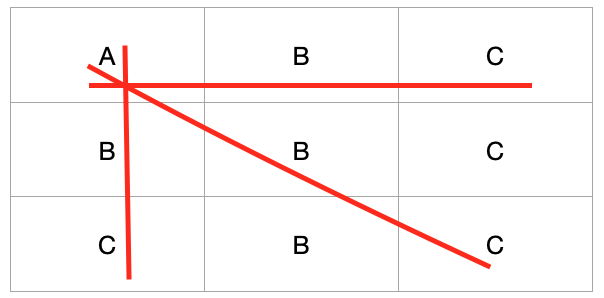
Given a 2-dimensional ‘board’ of characters, find the number of occurrences of a given string in that board. Matches can be found: left-right horizontally, top-bottom vertically or top left - bottom right diagonally. Matches of the given string value can overlap each other. So, for example, given the board below and the string “ABC”, there are 3 matches:
Solution:
from typing import List
def word_count(board: List[List[str]], word: str) -> int:
"""For a given 2-dimensional 'board' of characters, represented by a list of lists, calculate
the number of times a given word appears in the board, either horizontally, vertically, or diagonally
(left-to-right)
Parameters
----------
board : List[List[str]]
A 2-D 'board' of letters, represented by a list of (string) lists, e.g.
[["A", "B" "C"],
["B", "B", "C"],
["C", "B", "C"]]
word : str
word to 'search' for in board, e.g. "ABC"
Returns
-------
int
Count of times word appears in board, e.g. 3
"""
board_length = len(board[0])
board_height = len(board)
total_count = 0
# loop through horizontal arrays
if len(word) <= board_length:
for arr in board:
total_count += count_str_in_arr(arr, word)
# loop through vertical
if board_height >= len(word):
for i in range(board_length):
vert_arr = []
for arr in board:
vert_arr.append(arr[i])
total_count += count_str_in_arr(vert_arr, word)
# logic to create diagonal arrays - iterate over all top rows and columns on left of board
# loop through number of rows in board
for l in range(board_length):
# loop positions in row
for h in range(board_height):
# don't want to repeat elements
if l >= 1 and h > 0:
continue
diag_arr = []
# logic to create diagonal array given a starting point
for j, arr in zip(range(board_length), board[l:]):
if j+h <= board_length - 1:
diag_arr.append(arr[j+h])
# save some time ...no point checking if word not long enough
if len(diag_arr) >= len(word):
total_count += count_str_in_arr(diag_arr, word)
return total_count
def count_str_in_arr(arr: List[str], word: str) -> int:
"""Count the number of occurences of a word in a list of letters. Word occurences can be overlapping
Parameters
----------
arr : List[str]
An array of individual letters, e.g. ["A", "B", "C", "A", "B", "C"]
word : str
word to 'search' for in board, e.g. "ABC"
Returns
-------
int
Count of times word appears in array, e.g. 2
"""
arr_str = ''.join(arr)
occurences = 0
for i in range(len(arr_str)):
if arr_str[i:i+(len(word))] == word:
occurences +=1
return occurences
https://gist.github.com/jcalcutt/8e592d071f71eb80ead0ac546342bab3
I split my solution up into 3 distinct ‘sections’ - one to deal with each direction we can match the string. The focus of each ‘section’ is to create and pass all possible alignments of characters (i.e. an array) for that specific direction to a common helper function which counts the number of occurrences the string appears.
Of course, the horizontal implementation of this was fairly trivial, we have the arrays already created for us, and just need to loop through them. The vertical arrays were slightly more difficult, which involves just looping over the matrix, creating a new vertical array by indexing a particular value for each board loop.
The left-right diagonal creation of these arrays was the most difficult. I’m sure I haven’t implemented the ‘best’ solution here, but I’ll explain my thinking. Left-right diagonals can start anywhere along the top row and anywhere along the left side column, so, first we need to iterate over these matrix cells.
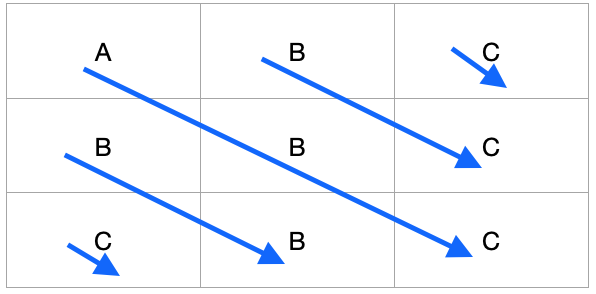
Once we have some logic to do this, for a given starting point, we can then build up a diagonal array by adding cells which are one row down and one column across from this starting cell (and the then the cell that came before it, etc). To save us some time, once we’ve created a diagonal array, we can check if it’s shorter than the length of the word we’re trying to match - if so, we can discard it, otherwise we can then implement the word count helper function. Finally, we return the running total we’ve been keeping track of.
Written on April 24th, 2021 by Jordan Calcutt